승쨩개발공부
[BJ] 1629 - 곱샘 (재귀기초, 모듈러 성질, 귀납적사고) 본문
[BJ] 1629 - 곱샘 (재귀기초, 모듈러 성질, 귀납적사고)
SeungHyune 2025. 3. 6. 01:06
0. 수학적 귀납법
내가 재귀를 풀떄마다 절차지향적으로 항상 생각했는데, 이젠 수학적 귀납법으로 생각을 해야한다.
도미노가있다 그러면 절차지향적 사고와 수학적 귀납법 사고를 생각해보자
1) 절차 지향적 사고
1번 도미노가 쓰러지면 2번 도미노도 쓰러지고 2번 도미노가 쓰러지면 3번 도미노도 쓰러진다.
1 -> 2 -> 3 -> 4 -> .... 이런식으로 모든 도미노가 쓰러진다 이건 절차지향적인 생각이다.
2) 수학적 귀납법 사고
1번 도미노가 쓰러진다 K번 도미노가 쓰러지면 K + 1번 도미노도 쓰러진다.
이것이 수학적 귀납법 사고이다.
1. 문제 설명
A^B % C (A^B mod C) 를 구하는건데 입력 조건을 보면 A,B,C모두 최대범위가 int의 최대 범위이다
즉 약 21억^21억을 한 변수에 담을 수 있을까? 불가능 하다
또한 그저 A에 B를 계속해서 곱해서 값을 받는방식은
최악의경우 21억번을 연산하기에 0.5초안에 불가능할것이다.
이떈 모듈러의 성질을 이용해야하는데.
A^B * A^B = A^2B이다 예를 들어 5의 6승은 5를 6개 곱한 것(5*5*5*5*5*5)이기 때문에
5*5*5*5*5*5 = (5*5*5) * (5*5*5) = 5^3 * 5^3 으로 생각할 수 있다.
(5^6) = 15,625 (5^3) * (5^3) = 15,625 두 값은 같다
그러면 12^116 = 12^58 * 12^58이기 때문에 12^58 = 4란걸 알면 12^116 = 4*4 = 16임을 알 수 있다.
위에서 말한 수학적 귀납법 사고로 설명하자면.
1번 도미노가 쓰러진다 K번 도미노가 쓰러지면 K + 1번 도미노도 쓰러진다.
이걸 이 문제로 풀어본다면
K승을 계산했으면 2K승과 2K + 1승을 구할 수 있다.
2K + 1 승은 어떻게?
2K승에 A를 곱해준다면 2K + 1승이 되니까.
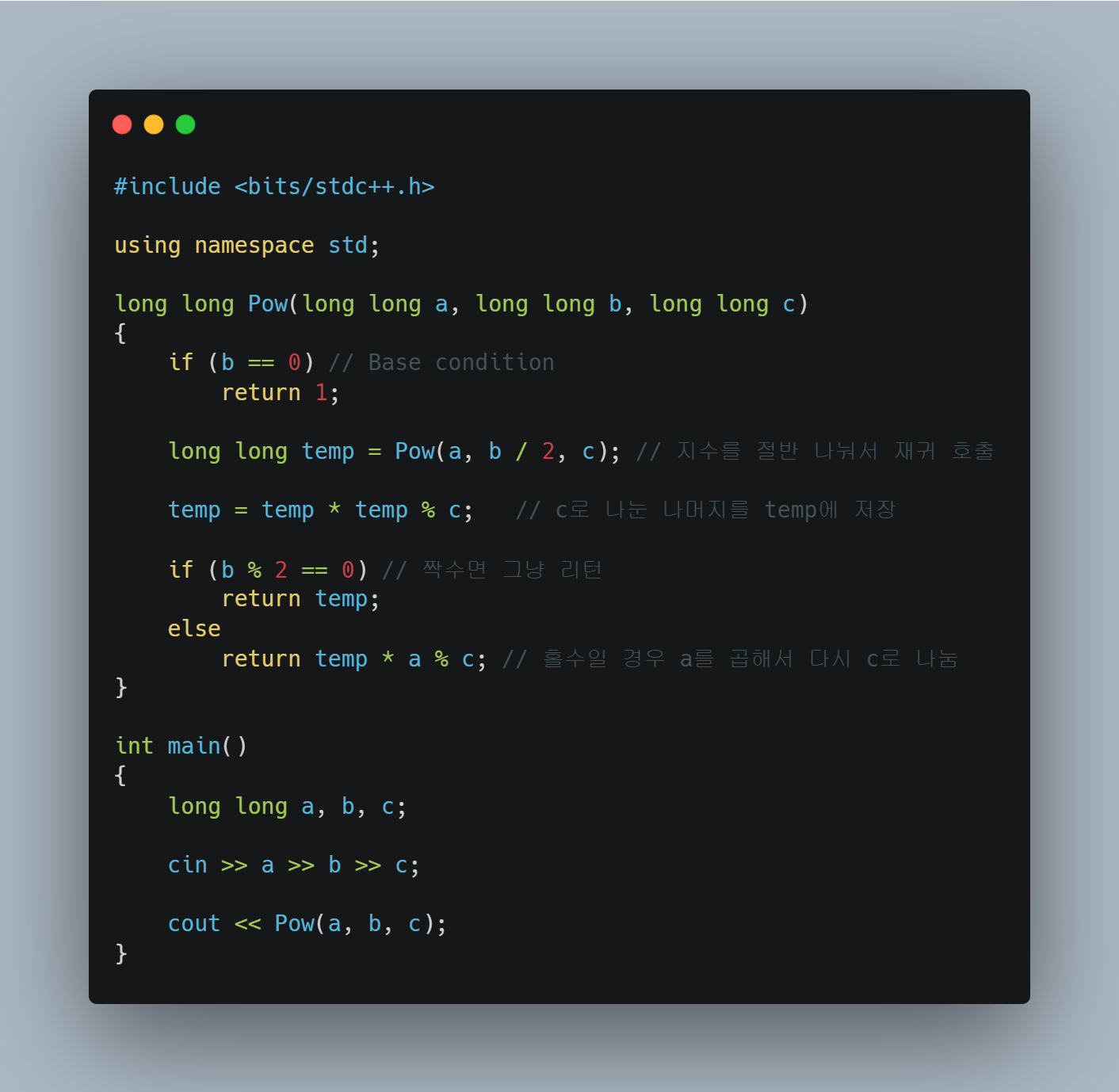
이처럼 재귀함수를 잘 짜려면 귀납적인 사고
즉 BaseCondition(재귀의 무한루프를 막는 조건) 을 잘 잡고 2K, 2K + 1승을 구할 수 있으니 마치 도미노를
쓰러트리는 것 처럼 모든 값이 제대로 계산될것이다 라고 함수를 이해할 필요가 있다.
즉 귀납법을 이용해 식을 세우고 나머지는 컴퓨터에게 맡기기만하면 끝이다 절차적으로 어떻게 프로그램이 흘러가는지는 전혀 신경 안써도 된다고 볼 수 있겠다.
트리 순회 이런것만 하다가 이런식으로 재귀를 푸니까 머리가 꺠질것같은데 앞으로 사고를 좀 바꿔야겠다
익숙해지면 매우 편할듯
'CodingTestTraining > BaekJoon(Basic)' 카테고리의 다른 글
| [BJ] 1260 - DFS와 BFS (그래프) (0) | 2025.10.28 |
|---|---|
| [BJ] 2568 - 안전 영역 (DFS 모든 경우의 수) (0) | 2025.10.28 |
| [BJ] 1926 - 그림 (BFS) (0) | 2025.02.24 |
| [BJ] 10866 - 덱(Deque) (0) | 2025.02.19 |
| [BJ] 15845 - 큐 (0) | 2025.02.19 |


